In this article named “Variation of Wind Velocity with Height”, how wind speed change as a function of structure height is discussed.
The viscosity of air reduces its velocity adjacent to the earth’s surface to almost zero, as shown in Figure 1. A retarding effect occurs in the wind layers near the ground, and these inner layers in turn successively slow the outer layers. The slowing down is reduced at each layer as the height increases, and eventually becomes negligibly small.
The height at which velocity ceases to increase is called the gradient height, and the corresponding velocity, the gradient velocity. This characteristic of variation of wind velocity with height is a well-understood phenomenon, as evidenced by higher design pressures specified at higher elevations in most building codes.
At heights of approximately 1200 ft (366 m) above ground, the wind speed is virtually unaffected by surface friction, and its movement is solely dependent on prevailing seasonal and local wind effects. The height through which the wind speed is affected by topography is called the atmospheric boundary layer. The wind speed profile within this layer is given by
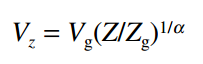
where
Vz = mean wind speed at height Z aboveground
Vg= gradient wind speed assumed constant above the boundary layer
Z = height aboveground
Zg= nominal height of boundary layer, which depends on the exposure (Values for Zg are given in Fig. 1.1.)
α = power law coefficient
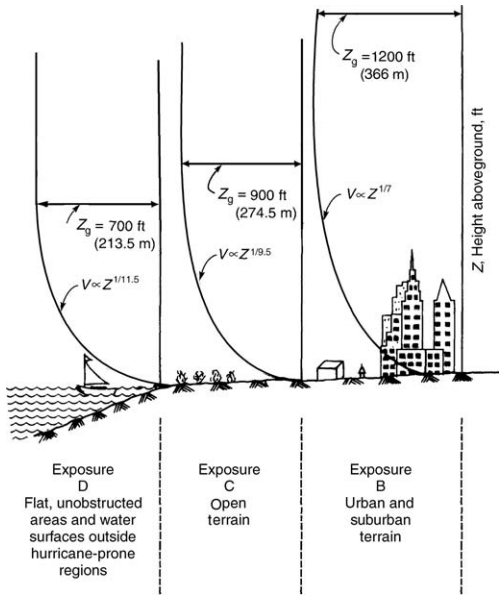
With known values of mean wind speed at gradient height and exponent α, wind speeds at height Z are calculated by using Eq. (1). The exponent 1/α and the depth of boundary layer Zg vary with terrain roughness and the averaging time used in calculating wind speed. α ranges from a low of 0.087 for open country of 0.20 for built-up urban areas, signifying that wind speed reaches its maximum value over a greater height in an urban terrain than in the open country
