Calculation of Loads and Pressures on Concrete Formwork

In concrete construction, forms are extremely important as they mold the concrete to the required size
and shape. When it comes to construction, forms have to be designed properly to provide safe support to loads incurred during the process of building.

The possible loads that might act on formwork are many. In this article, these types of loads are outlined along with the method of their calculation.

1- Vertical Loads

Vertical loads acting on the formwork include the self-weight of the forms, the placed reinforcement, the weight of fresh concrete, the weight of the workers, and the weight of placing equipment and tools.

For concretes with normal reinforcement ratios, the dead load is usually estimated at 22 to 25 kN/m³. Thus, an 16 cm normal weight slab would exert a dead load of 25 kN/m³ x 0.16 m = 4 kN/m² on a horizontal formwork. However, in cases where the reinforcement appears to be heavy, the weights of materials should be computed separately to determine the actual unit weight.

The American Concrete Institute, ACI Committee 347, states that horizontal formworks should be designed for a minimum vertical live load of 2.39 kPa to account for the loads of workers and their tools such as vibrators and screeds. This value is increased to 3.59 kPa if motorized carts or buggies are utilized.

Additionally, ACI recommends that the minimum combined total design dead and live load should not be less than 4.79 kPa or 6 kPa when using motorized buggies.

Finally, the own weight of formwork is determined by using the unit weight of its material and the exact dimensions of its various parts. It is worth noting that the weight of formworks is far less than the dead load of the concrete and the construction live loads. Therefore, an allowance is assumed as superimposed load per square meter.

At the beginning of formwork design, the engineer can assume an initial weight for the formwork between 0.24-0.72 kPa as a starting value. Then, this value is checked and revised when the exact members’ sizes are determined.

2- Lateral Pressures of Concrete on Formwork

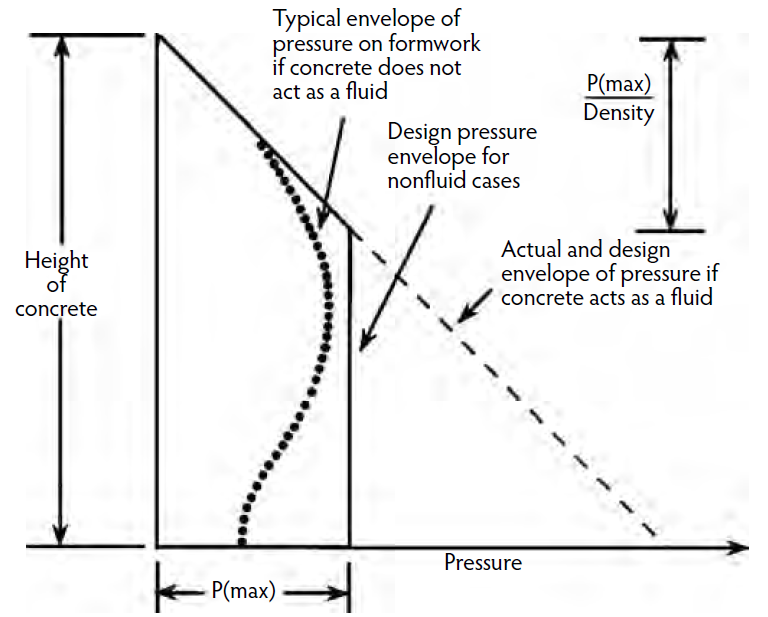
Unlike horizontal formworks, vertical formworks, such as those for walls and columns, are subjected to internal lateral pressure from the accumulated depth of concrete placed. When placing, fresh concrete near the top or sometimes at greater depths acts as a liquid during vibration and generates lateral pressures equal to the vertical liquid head.

On contrast, the lateral pressures are less than the liquid head at depths below the controlled depth of vibration due to many factors. For instance, for a slow vertical placement rate, the concrete mass in the lower part has the time to start setting and stiffening. The friction between concrete and form, migration of pore water, and other factors may also reduce the resulting lateral pressures.

The next figure indicates the distribution of the pressures as revealed by tests. The pressure starts as a liquid pressure near the top and reaching a maximum at some lower level. In the design practice, this maximum value is usually assumed for the rest of the height. This is a conservative approach.

Typical and assumed distributions of concrete lateral pressure.

ACI Committee 347 stated that the following equation can be used to calculate the concrete lateral pressure if the slump of fresh concrete slump value is greater than 175 mm and it was not placed with normal internal vibration to a depth of 1.2 m or less:

P = ρgh ; where:

P: Lateral pressure of concrete, kPa – : Concrete density, Kg/m³– g: Gravity acceleration, 9.81 m²/s – h: Depth of plastic concrete from placement location to the specified point, m

For concretes with a slump value of less than 175 mm and placed with normal vibration to a depth of 1.2 m or less, ACI Committee 347 defines the lateral pressure of concrete as:

a- For Columns (vertical elements with no plan dimensions surpass 2 m)

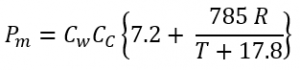
with minimum of 30C_w kPa and not greater than ρgh.

where:

P_m: Maximum lateral pressure of concrete, kPa – C_w: Coefficient of unit weight (described below) – C_c: Coefficient of chemistry (described below) – R: Concrete placement rate, m/h – T: Concrete temperature at placing, ^oC

b- For Walls (vertical elements with at least one plan dimension larger than 2 m)

This case is for walls with placement rate of less than 2.1 m/h and a placement height equal or less than 4.2 m.

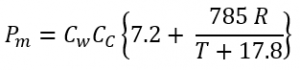
with minimum of 30C_w kPa and not greater than ρgh

c- For Walls (vertical elements with at least one plan dimension larger than 2 m)

This case is for walls with placement rate of greater than 2.1 m/h and a placement height greater than 4.2 m.

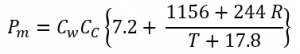
with minimum of 30C_w kPa and not greater than ρgh

Next the values of C_w and C_c are given:

Unit weight of concrete	C_w
Less than 2240 Kg/m³	C_w=0.5[1+(w/2320 Kg/m³)] but not less than 0.80
2240 to 2400 Kg/m³	1.0
More than 2400 Kg/m³	C_w=w / 2320 Kg/m³

Cement type	C_c
Type I, II, and III without retarders^a	1.0
Type I, II, and III with a retarder^a	1.2
Other types or blends containing less than 70 percent slag or 40 percent fly ash without retarders^a	1.2
Other types or blend containing less than 70 percent slag or 40 percent fly ash with a retarder¹	1.4
Blends containing more than 70 percent slag or 40 percent fly ash	1.4

^aRetarders include any admixture, such as a retarder, retarding water reducer, retarding mid-range water reducing admixture, or high-range water-reducing admixture (superplasticizer), that delays setting of concrete.

To complete the picture, the pressure that acts on the column forms is transferred to the external tie elements on the adjacent sides of the form. Also, for walls, it is transferred from plywood, studs, or wales to the tension ties that link the two opposite sides of the form. The following figures illustrates some elements that are essential for resisting the external lateral pressure that tends to overturn the wall, column, or slab forms.

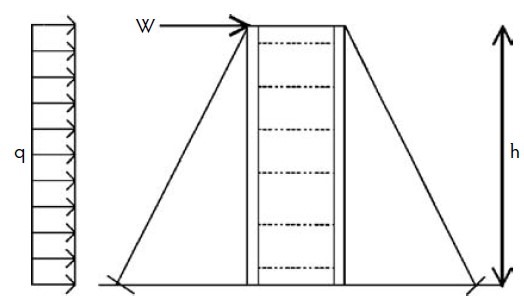
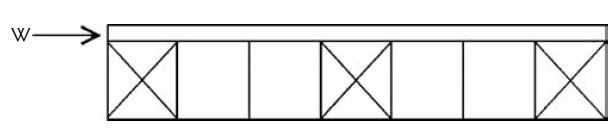
3- Horizontal Loads on Formworks

Horizontal loads are caused by forces such as wind loads, seismic loads, inclined supports, and inclined dumping of concrete.

ACI Committee 347 recommends the minimum horizontal loads for design to prevent lateral collapse of the formwork to be of the greater of :

1.5 kN per linear meter of floor edge or;

2% of total dead load on the form distributed as a uniform load per meter of slab edge

For wall forms, bracing should be designed to meet the minimum wind load requirements of ASCE 7-05 with wind velocity adjustment for shorter recurrence interval as provided in ASCE 37-02.