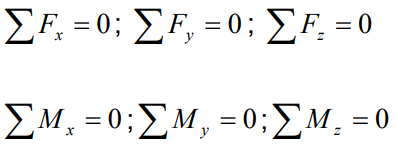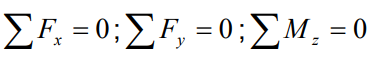Equations of Static Equilibrium
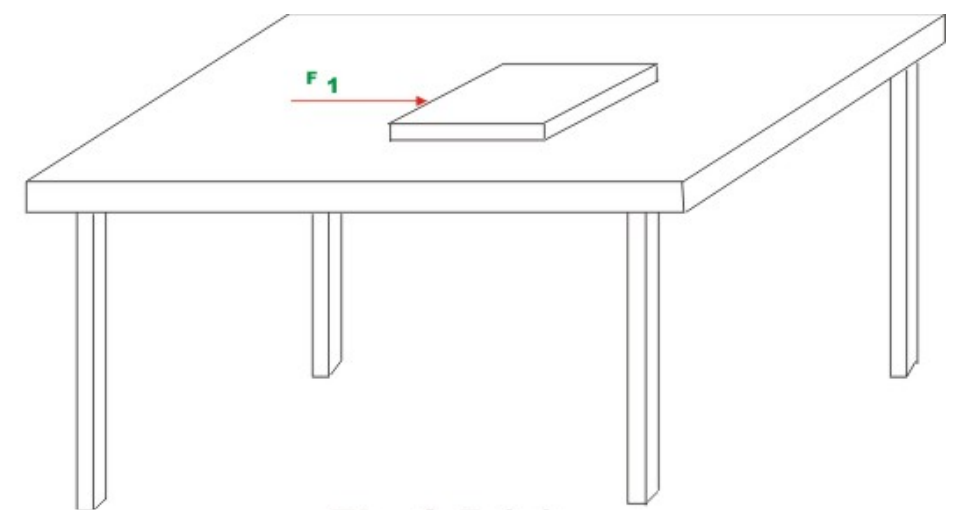
Equations of Static Equilibrium: Consider a case where a book is lying on a frictionless table surface. Now, if we apply a force F1 horizontally as shown in the Fig.1(a), then it starts moving in the direction of the force. However, if we apply the force perpendicular to the book as in Fig. 1 (b), then book stays in the same position, as in this case the vector sum of all the forces acting on the book is zero. When does an object move and when does it not? This question was answered by Newton when he formulated his famous second law of motion. In a simple vector equation it may be stated as follows:
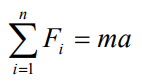
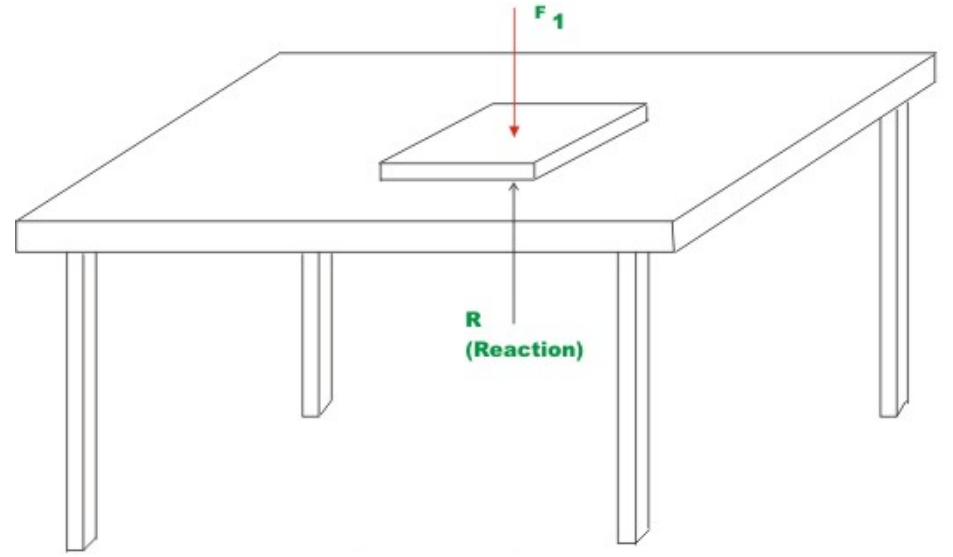
where
is the vector sum of all the external forces acting on the body,
m is the total mass of the body and is the acceleration vector. However, if the body is in the state of static equilibrium then the right hand of equation (1) must be zero. Also for a body to be in equilibrium, the vector sum of all external moments () about an axis through any point within the body must also vanish. Hence, the book lying on the table subjected to external force as shown in Fig. 1 (b) is in static equilibrium. The equations of equilibrium are the direct consequences of Newton’s second law of motion. A vector in 3-dimensions can be resolved into three orthogonal directions viz., x, y and z (Cartesian) coordinate axes. Also, if the resultant force vector is zero then its components in three mutually perpendicular directions also vanish. Hence, the above two equations may also be written in three co-ordinate axes directions as follows:
Now, consider planar structures lying in xy − plane. For such structures we could have forces acting only in x and y directions. Also the only external moment that could act on the structure would be the one about the z -axis. For planar structures, the resultant of all forces may be a force, a couple or both. The static equilibrium condition along x -direction requires that there is no net unbalanced force acting along that direction. For such structures we could express equilibrium equations as follows:
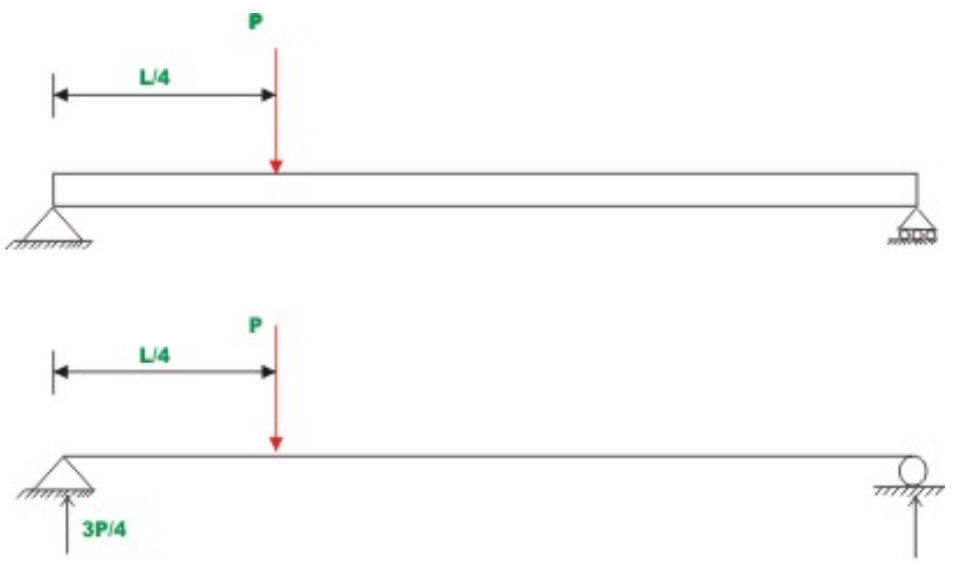
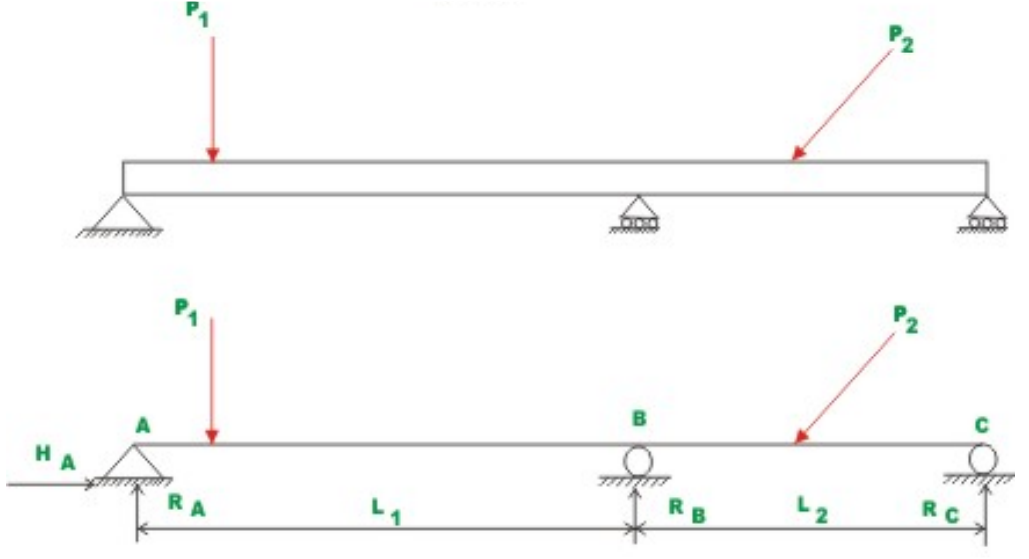
Using the above three equations we could find out the reactions at the supports in the beam shown in Fig. 2. After evaluating reactions, one could evaluate internal stress resultants in the beam. Admissible or correct solution for reaction and internal stresses must satisfy the equations of static equilibrium for the entire structure. They must also satisfy equilibrium equations for any part of the structure taken as a free body. If the number of unknown reactions is more than the number of equilibrium equations (as in the case of the beam shown in Fig. 3), then we can not evaluate reactions with only equilibrium equations. Such structures are known as the statically indeterminate structures. In such cases we need to obtain extra equations (compatibility equations) in addition to equilibrium equations.
Read About: